Bemerkungen

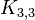
Bild: Life of Riley


Bild: Life of Riley
Wenn (so wie in der Realität häufig der Fall) ein Land auf mehrere nicht-angrenzende Gebiete verteilt ist (Kolonien, Exklaven,…), dann ist der zugehörige Graph nicht notwendigerweise planar und es sind möglicherweise mehr als vier Farben zur Färbung notwendig. Auf Planarität kann man gegebene Graphen sehr schnell testen. Nach dem Satz von Kuratowski gibt es bestimmte Untergraphen, die die Planarität von Graphen verhindern. Es sind dies genau zwei Grundformen, die sogenannten Kuratowski-Minoren  und
und 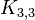 , und darüber hinaus ihre Unterteilungen. Durch eine geschickte Wahl der Datenstrukturen kann man diese „Untergraphen“ finden bzw. feststellen, dass es sie nicht gibt, indem man jeden Knoten und jede Kante nur konstant oft betrachtet.
, und darüber hinaus ihre Unterteilungen. Durch eine geschickte Wahl der Datenstrukturen kann man diese „Untergraphen“ finden bzw. feststellen, dass es sie nicht gibt, indem man jeden Knoten und jede Kante nur konstant oft betrachtet.
Die kleinste mögliche Färbung in allgemeinen Graphen  zu finden, mit anderen Worten die sogenannte Chromatische Zahl
zu finden, mit anderen Worten die sogenannte Chromatische Zahl  zu bestimmen, ist sehr aufwändig (genauer: eine NP-vollständige Aufgabe). Nach den Aussagen von Tutte wäre sie gelöst, wenn man im Dualgraphen
zu bestimmen, ist sehr aufwändig (genauer: eine NP-vollständige Aufgabe). Nach den Aussagen von Tutte wäre sie gelöst, wenn man im Dualgraphen 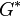 eine kleinste Gruppe gefunden hat, sodass eine gruppenwertige Strömung (das ist ein „Fluss ohne Anfang und Ende“), die nirgends das Nullelement annimmt, existiert. Diese Gruppenordnung heißt Flusszahl
eine kleinste Gruppe gefunden hat, sodass eine gruppenwertige Strömung (das ist ein „Fluss ohne Anfang und Ende“), die nirgends das Nullelement annimmt, existiert. Diese Gruppenordnung heißt Flusszahl  und es ist für beliebige Graphen
und es ist für beliebige Graphen  . Die Lösbarkeit dieses nach wie vor NP-vollständigen Problems ist unabhängig von der Struktur der vorgegebenen Gruppe und hängt nur von der Gruppenordnung ab.[2]
. Die Lösbarkeit dieses nach wie vor NP-vollständigen Problems ist unabhängig von der Struktur der vorgegebenen Gruppe und hängt nur von der Gruppenordnung ab.[2]
Es gibt weitere Zusammenhänge des Vier-Farben-Problems mit Problemen der Diskreten Mathematik, sodass man auch Methoden der Algebraischen Topologie anwenden kann.
Dieser Artikel basiert auf dem Artikel Vier-Farben-Satz aus der freien Enzyklopädie Wikipedia und steht unter der Doppellizenz GNU-Lizenz für freie Dokumentation und Creative Commons CC-BY-SA 3.0 Unported (Kurzfassung). In der Wikipedia ist eine Liste der Autoren verfügbar. |